la tecnologia y la matematicas

QUE SON SUCESIONES

Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.

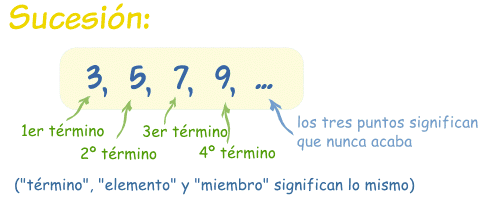Finita o infinita

Si la sucesión sigue para siempre, es una sucesión infinita,
si no es una sucesión finita

Ejemplos

{1, 2, 3, 4 ,...} es una sucesión muy simple (y es una sucesión infinita)

{20, 25, 30, 35, ...} también es una sucesión infinita

{1, 3, 5, 7} es la sucesión de los 4 primeros números impares (y es una sucesión infinita)

{4, 3, 2, 1} va de 4 a 1 hacia atrás

{1, 2, 4, 8, 16, 32, ...} es una sucesión infinita donde vamos doblando cada término

{a, b, c, d, e} es la sucesión de las 5 primeras letras en order alfabético

{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre "alfredo"

{0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s (sí, siguen un orden, en este caso un orden alternativo)

En orden

Cuando decimos que los términos están "en orden", ¡nosotros somos los que decimos qué orden! Podría ser adelante, atrás... o alternando... ¡o el que quieras!

Una sucesión es muy parecida a un conjunto, pero con los términos en orden (y el mismo valor sí puede aparecer muchas veces).

Ejemplo: {0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s. El conjunto sería sólo {0,1}

La regla

Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.

Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:

{3, 5, 7, 9, ...}

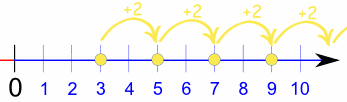
¡Pero la regla debería ser una fórmula!

Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:

10º término,
100º término, o
n-ésimo término (donde n puede ser cualquier número positivo que queramos).

Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).

Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?

Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:

Probamos la regla: 2n

n	Término	Prueba
1	3	2n = 2×1 = 2
2	5	2n = 2×2 = 4
3	7	2n = 2×3 = 6

Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:

Probamos la regla: 2n+1

n	Término	Regla
1	3	2n+1 = 2×1 + 1 = 3
2	5	2n+1 = 2×2 + 1 = 5
3	7	2n+1 = 2×3 + 1 = 7

¡Funciona!

Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como

La regla para {3, 5, 7, 9, ...} es: 2n+1

Ahora, por ejemplo, podemos calcular el término 100º: 2 × 100 + 1 = 201

Notación

Para que sea más fácil escribir las reglas, normalmente lo hacemos así:

Posición del término

Es normal usar x_n para los términos:

x_n es el término
n es la posición de ese término

Así que para hablar del "quinto término" sólo tienes que escribir: x₅

Entonces podemos escribir la regla para {3, 5, 7, 9, ...} en forma de ecuación, así:

x_n = 2n+1

Ahora, si queremos calcular el 10º término, podemos escribir:

x₁₀ = 2n+1 = 2×10+1 = 21

¿Puedes calcular el 50º término? ¿Y el 500º?

Ahora veamos algunas sucesiones especiales y sus reglas:

Tipos de sucesiones

Sucesiones aritméticas

El ejemplo que acabamos de usar, {3,5,7,9,...}, es una sucesión aritmética (o progresión aritmética), porque la diferencia entre un término y el siguiente es una constante.

Ejemplos

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

Esta sucesión tiene una diferencia de 3 entre cada dos términos.
La regla es x_n = 3n-2

3, 8, 13, 18, 23, 28, 33, 38, ...

Esta sucesión tiene una diferencia de 5 entre cada dos términos.
La regla es x_n = 5n-2

Sucesiones geométricas

En una sucesión geométrica cada término se calcula multiplicando el anterior por un número fijo.

Ejemplos:

2, 4, 8, 16, 32, 64, 128, 256, ...

Esta sucesión tiene un factor 2 entre cada dos términos.
La regla es x_n = 2ⁿ

3, 9, 27, 81, 243, 729, 2187, ...

Esta sucesión tiene un factor 3 entre cada dos términos.
La regla es x_n = 3ⁿ

4, 2, 1, 0.5, 0.25, ...

Esta sucesión tiene un factor 0.5 (un medio) entre cada dos términos.
La regla es x_n = 4 × 2^-n

Sucesiones especiales

Números triangulares

1, 3, 6, 10, 15, 21, 28, 36, 45, ...

Esta sucesión se genera a partir de una pauta de puntos en un triángulo.
Añadiendo otra fila de puntos y contando el total encontramos el siguiente número de la sucesión.

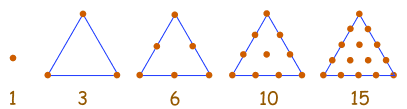
números triangulares

Pero es más fácil usar la regla

x_n = n(n+1)/2

Ejemplo:

El quinto número triangular es x₅ = 5(5+1)/2 = 15,
y el sexto es x₆ = 6(6+1)/2 = 21

Números cuadrados

1, 4, 9, 16, 25, 36, 49, 64, 81, ...

El siguiente número se calcula elevando al cuadrado su posición.

La regla es x_n = n²

Números cúbicos

1, 8, 27, 64, 125, 216, 343, 512, 729, ...

El siguiente número se calcula elevando al cubo su posición.

La regla es x_n = n³

Números de Fibonacci

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

El siguiente número se calcula sumando los dos que están antes de él.
El 2 se calcula sumando los dos delante de él (1+1)
El 21 se calcula sumando los dos delante de él (8+13)

La regla es x_n = x_n-1 + x_n-2

Esta regla es interesante porque depende de los valores de los términos anteriores.

Por ejemplo el 6º término se calcularía así:

x₆ = x_6-1 + x_6-2 = x₅ + x₄ = 5 + 3 = 8

Series

"Sucesiones" y "series" pueden parecer la misma cosa... pero en realidad una serie es la suma de una sucesión.

Sucesión: {1,2,3,4}

Serie: 1+2+3+4 = 10

Las series se suelen escribir con el símbolo Σ que significa "súmalos todos":

	Esto significa "suma de 1 a 4" = 10

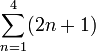	Esto significa "suma los cuatro primeros términos de la sucesión 2n+1" Que son los cuatro primeros términos de nuestro ejemplo {3,5,7,9,...} = 3+5+7+9 = 24

Definición

Sucesión monótona creciente

Una sucesión es monótona creciente si se cumple que para todo n natural a_n <= a_n+1 (a₁ <= a₂ <= a₃ <= ... <= a_n).

Ejemplo:

a_n = n es monótona creciente.

a₁ = 1, a₂ = 2, a₃ = 3, a₄ = 4, ...

Definición

Sucesión monótona decreciente

Una sucesión es monótona decreciente si se cumple que para todo n natural a_n >= a_n+1 (a₁ >= a₂ >= a₃ >= ... >= a_n).

Ejemplo:

a_n = 1/n es monótona decreciente.

a₁ = 1, a₂ = 1/2, a₃ = 1/3, a₄ = 1/4, ...

Límite finito de una sucesión

Consideremos la sucesión a_n = 1/n.

a₁ = 1
a₂ = 1/2 = 0.5
a₃ = 1/3 ≈ 0.33
a₄ = 1/4 = 0.25
a₅ = 1/5 = 0.2
a₆ = 1/6 ≈ 0.17
a₇ = 1/7 ≈ 0.14
a₈ = 1/8 ≈ 0.12
a₉ = 1/9 ≈ 0.11
a₁₀ = 1/10 = 0.1

A medida que aumenta n, los términos de la sucesión son cada vez más cercanos a 0. Si representamos los términos como puntos en una línea, esto significa que los puntos a_n se apiñan cada vez más cerca del punto 0 conforme n crece.

Sucesión con límite 0

Se dice que a_n tiende a 0, o que tiene límite 0.
Se expresa simbólicamente por: lim a_n = 0 o bien, ocasionalmente, por la notación abreviada a_n -> 0.

Definición

Límite finito

lim a_n = a <=> para todo ε>0 existe N natural / para todo n > N a - ε < a_n < a + ε, o lo que es lo mismo, |a_n - a| < ε.

Para cualquier número positivo ε, por pequeño que sea, podemos encontrar un natural N suficientemente grande tal que a partir del índice N en adelante se tiene que |a_n - a| < ε.
Es decir, si tomamos un entorno de a de cualquier radio siempre habrá un subíndice N tal que desde N en adelante todos los términos de la sucesión pertenecen a dicho entorno.

Límite infinito de una sucesión

Consideremos la sucesión a_n = n².

a₁ = 1
a₂ = 4
a₃ = 9
a₄ = 16
...
a₁₀ = 100
...
a₁₀₀ = 10.000

Al crecer n, a_n no tiende a un límite definido, sino que crece más allá de toda cota. Se dice que a_n tiende a infinito.

Definición

Límite infinito

lim a_n = +inf <=> para todo K>0 existe N natural / para todo n > N a_n > K.

Para cualquier número positivo K (tan grande como se quiera), podemos encontrar un natural N, tal que a_N y todos los términos siguientes son mayores que K. Esto quiere decir que a_n puede hacerse mayor que cualquier cota, con tal de que n sea lo suficientemente grande.

Del mismo modo se define lim a_n = -inf <=> para todo K<0 existe N natural / para todo n > N a_n < K.

Definición

Convergencia y divergencia

Cuando una sucesión tiene límite finito a se dice que es convergente y converge a a.
Una sucesión que tiene límite infinito se llama divergente.
Una sucesión que carece de límite se llama oscilante.

La sucesión a_n = 1/n converge a 0.
La sucesión a_n = n² es divergente.
La sucesión a_n = sen n es oscilante, pues sus valores varían entre 1 y -1.

Propiedades del límite finito de sucesiones

Unicidad del límite

Si una sucesión tiene límite es único.

H) lim a_n = b
T) b es único

Demostración:

La demostración se hace por reducción al absurdo.
Suponemos que a_n tiene dos límites distintos b y c.
Suponemos que b > c.

lim a_n = b => (por def. de límite finito de una sucesión) para todo ε>0 existe n₁ natural / para todo n > n₁b - ε < a_n < b + ε;

lim a_n = c => (por def. de límite finito de una sucesión) para todo ε>0 existe n₂ natural / para todo n > n₂c - ε < a_n < c + ε

Consideremos un ε tal que c+ε < b-ε, o sea ε < (b - c)/2

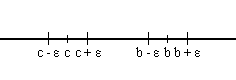
Sea N = max {n₁,n₂}

Para todo n > N se cumple

b - ε < a_n < b + ε
c - ε < a_n < c + ε

Absurdo, pues a_n no puede pertenecer a dos entornos disjuntos.
Absurdo de suponer b ≠ c.
Por lo tanto b = c.

Límite de la sucesión comprendida

Si una sucesión está comprendida entre otras dos que tienen igual límite, entonces tiene el mismo límite.

H) lim a_n = lim b_n = p
Para todo n > n₀ a_n <= c_n <= b_n
T) lim c_n = p

Demostración:

lim a_n = p => (por def. de límite de una sucesión) para todo ε₁ > 0 existe n₁ natural / para todo n > n₁p - ε₁ < a_n < p + ε₁

lim b_n = p => (por def. de límite de una sucesión) para todo ε₂ > 0 existe n₂ natural / para todo n > n₂p - ε₂ < b_n < p + ε₂

Sea N = max {n₀, n₁, n₂}

Para todo n > N se cumple p-ε₁ < a_n <= c_n <= b_n < p+ε₂

p-ε₁ < c_n < p+ε₂

Sea ε = min {ε₁, ε₂}

Para todo n > N p-ε < c_n < p+ε

=> (por def. de límite de una sucesión) lim c_n = p.

Operaciones con límites

El límite de la suma, producto y cociente de sucesiones se determina por las mismas reglas que para las funciones de variable continua. Las demostraciones son iguales, basta sustituir f(x) por a_n y considerar que la tendencia siempre es hacia +infinito. Aquí sólo demostraremos el límite de una suma. Para ver las demás reglas visitar la página sobreoperaciones con límites.

Límite de la suma

Si dos sucesiones tienen límite finito, entonces su suma tiene límite finito y es igual a la suma de esos límites.

H) lim a_n = a, lim b_n = b
T) lim a_n + b_n = a + b

Demostración:

Queremos probar que, dado ε > 0, existe N > 0 tal que para todo n > N |(a_n + b_n) - (a+b)| < ε.

Sea ε' = ε/2

lim a_n = a => (por def. de límite finito de una sucesión) para todo ε' > 0 existe n₀ natural / para todo n > n₀ |a_n - a| < ε'.

lim b_n = b => (por def. de límite finito de una sucesión) para todo ε' > 0 existe n₁ natural / para todo n > n₁ |b_n - b| < ε'.

Sea N = max {n₀, n₁}

Para todo n > N se cumple:

|a_n - a| < ε'
|b_n - b| < ε'

=> |a_n - a| + |b_n - b| < 2ε' = ε

|(a_n + b_n) - (a+b)| = |(a_n - a) + (b_n - b)| <= (*) |a_n - a| + |b_n - b| < ε

(*) Desigualdad triangular: |x + y| <= |x| + |y|

Resumiendo, dado ε>0 existe N / para todo n > N |(a_n + b_n) - (a+b)| < ε

=> (por def. de límite finito de una sucesión) lim a_n + b_n = a + b

Definición

Sucesiones equivalentes

Dos sucesiones se dicen equivalentes cuando el límite de su cociente es 1.

Definición

Sucesión acotada

M es cota superior de la sucesión a_n si a_n < M para todo n.
m es cota inferior de la sucesión a_n si a_n > m para todo n.
Una sucesión es acotada si tiene tanto cota superior como inferior.

Teorema

Toda sucesión monótona y acotada converge.

H) a_n monótona
Existen m y M / m < a_n < M para todo n.
T) lim a_n = b

Demostración:

Queremos probar que existe N / para todo n > N |a_n - b| < ε.

Supongamos que a_n es creciente (si suponemos que es decreciente, la demostración es análoga).

a_n < M para todo n

Es decir que el conjunto de todos los términos de la sucesión S = {a₁, a₂, a₃, ...} tiene extremo superior (la menor de las cotas superiores), llamémosle b.

Sea ε>0

b - ε no es cota superior de S pues es menor que el extremo superior

=> existe N / a_N > b-ε.

a_n es creciente => para todo n > N a_n >= a_N => a_n > b-ε => -(a_n - b) < ε (1)

b+ε también es cota superior de S

=> para todo n a_n < (b+ε) => => a_n - b < ε (2)

=> De 1) y 2) para todo n > N |a_n - b| < ε

Teorema

Toda sucesión convergente es acotada.

H) a_n convergente
T) a_n acotada

Demostración:

a_n es convergente, eso significa que tiene límite finito: lim a_n = a

=> (por def. de límite finito de una sucesión) para todo ε>0 existe N / para todo n > N a-ε < a_n < a+ε

=> (por def. de sucesión acotada) a_n está acotada.

Nota: El recíproco no es cierto. Que una sucesión esté acotada no implica que sea convergente.

Contraejemplo: a_n = (-1)ⁿ está acotada pero no es convergente.

-1, 1, -1, 1, -1, 1, -1, 1, ...

Definición

Par de sucesiones monótonas convergentes

((a_n),(b_n)) es un par de sucesiones monótonas convergentes si
a) a_n es creciente y b_n decreciente.
b) Para todo n natural a_n <= b_n
c) Para todo ε>0 existe h natural / b_h - a_h < ε

Par de sucesiones monótonas convergentes

Ejemplo:

a_n = -1/n, b_n = 1/n

a_n es creciente.

Debemos probar que a_n+1 >= a_n, o sea a_n+1 - a_n >= 0

-1    -1    -n + n + 1     1
--- - --- = ---------- = ------ > 0
n+1    n      n(n+1)     n2 + n

b_n es decreciente.

Debemos probar que b_n+1 <= b_n, o sea b_n - b_n+1 >= 0

 1     1    n + 1 - n     1
--- - --- = --------- = ------ > 0
 n    n+1     n(n+1)    n2 + n

Para todo n a_n < b_n

-1     1
--- < --- pues -n < n para todo n.
 n     n

Dado ε>0, existe h / b_h - a_h < ε
```
 1    -1     2                          
--- - --- = --- < ε 
 h     h     h                          
```
Para que se cumpla basta tomar un h > 2/ε

Propiedad

Todo PSMC tiene frontera

((a_n),(b_n)) es un PSMC => existe c / para todo n a_n <= c <= b_n, lim a_n = c- y lim b_n = c+.

lim a_n = c- significa que a_n se aproxima a c por la izquierda, y lim b_n = c+ significa que b_n se aproxima a c por la derecha.

El número e

A menudo un número a se describe por medio de una sucesión infinita a_n de aproximaciones; esto es, el valor a está dado por el valor a_n con cualquier grado de precisión deseado si el índice n se elige suficientemente grande.

Este es el caso del número e (e = 2,718281...), que puede definirse como el límite de la sucesión a_n = (1 + 1/n)ⁿ o de la sucesión b_n = (1 + 1/n)ⁿ⁺¹.

Probaremos que estas sucesiones forman un PSMC.

a_n es creciente.

Demostración:

Utilizando la fórmula del binomio de Newton, podemos expresar (1+1/n)ⁿ como:

                                                          
                   n  n               n     n!        
an = (1 + 1/n)n  = Σ Ci.1n-i.(1/n)i = Σ   ---------- 
                  i=0                i=0 (n-i)!i!ni   

                                                            
                       n+1 n+1                  n+1    (n+1)!
an+1=(1 + 1/(n+1))n+1 = Σ  Ci.1n+1-i.(1/(n+1))i = Σ  ----------------
                       i=0                      i=0 (n+1-i)!i!(n+1)i

El desarrollo de a_n+1 tiene un término más que el de a_n y cada término es positivo. Si probamos que cada sumando de a_nes menor o igual que el correspondiente de a_n+1 probaremos que a_n es creciente.

   n!       ?      (n+1)!
---------- <= ---------------
(n-i)!i!ni    (n+1-i)!i!(n+1)i

n(n-1)...(n-i+1)  ? (n+1)(n)...(n+1-i+1)  --> i factores
---------------- <= --------------------
    n.n....n         (n+1)(n+1)...(n+1)   --> i factores
	
(n-1)   (n-i+1)  ?  n    n+1-i+1
-----...------- <= ---...-------
  n	   n       n+1     n+1
  
      1          i-1   ?       1          i-1
(1 - ---)...(1 - ---) <= (1 - ---)...(1 - ---)
      n           n           n+1         n+1

Cada factor es de la forma 1 - p/n donde p es el mismo en ambos miembros.

1 - p/n < 1 - p/(n+1)

Entonces cada factor del primer miembro es menor que el correspondiente del segundo.

Por lo tanto, cada sumando del desarrollo de a_n es menor que el correspondiente de a_n+1.

=> a_n es creciente.

b_n es decreciente.

bn = (1 + 1/n)n+1
bn+1 = (1 + 1/n+1)n+2 = (1 + 1/n+1)n+1.(1 + 1/n+1)
     ?
bn+1 <= bn
                           ?
(1 + 1/n+1)n+1.(1 + 1/n+1) <= (1 + 1/n)n+1

 (1 + 1/n)n+1   ?      1
-------------- >= 1 + ---
(1 + 1/n+1)n+1        n+1

   n+1/n   n+1   ?      1
( ------- )     >= 1 + ---
  n+2/n+1              n+1

  n2 + 2n + 1  n+1  ?      1
( ----------- )    >= 1 + ---
    n2 + 2n               n+1    
  
         1    n+1  ?      1
( 1 + ------- )   >= 1 + ---		
      n2 + 2n            n+1

Desigualdad de Bernoulli: (1+p)^q >= 1 + pq si p>=-1 y q>1

         1    n+1          n+1
( 1 + ------- )   >= 1 + -------		
      n2 + 2n            n2 + 2n
	  
      n+1  ?       1  
1 + ------ >= 1 + ---
    n2 + 2n       n+1
	
  n+1   ?   1
------- >= ---
n2 + 2n    n+1

n2 + 2n + 1 > n2 + 2n se cumple para todo n.

Para todo n a_n < b_n

an = (1 + 1/n)n
bn = (1 + 1/n)n+1

        ?
bn - an > 0
                      ?
(1+1/n)n+1 - (1+1/n)n > 0

Sacamos factor común:

(1+1/n)n(1+1/n - 1) = 1/n(1+1/n)n > 0 para todo n >= 1.

Dado ε>0 existe n natural / b_n - a_n < ε

                               (1)      (2)
bn - an = 1/n(1+1/n)n = (1/n)an < (1/n)bn < (1/n)b1 = (1/n)4 < ε

(1) a_n < b_n
(2) b_n decreciente

Basta elegir n > 4/ε

Por lo tanto, a_n y b_n forman un PSMC. El elemento frontera es el número e.

n=1:      2 < e < 4
n=2:   2,25 < e < 3,375
n=3:   2,37 < e < 3,16
n=4:   2,44 < e < 3,05
...
n=100: 2,70 < e < 2,73

Buscar en el sitio

Contacto

QUE SON SUCESIONES

Finita o infinita

Ejemplos

En orden

La regla

¡Pero la regla debería ser una fórmula!

Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?

Notación

Posición del término

Tipos de sucesiones

Sucesiones aritméticas

Ejemplos

Sucesiones geométricas

Ejemplos:

Sucesiones especiales

Números triangulares

Números cuadrados

Números cúbicos

Números de Fibonacci

Series

Definición

Sucesión monótona creciente

Definición

Sucesión monótona decreciente

Límite finito de una sucesión

Definición

Límite finito

Límite infinito de una sucesión

Definición

Límite infinito

Definición

Convergencia y divergencia

Propiedades del límite finito de sucesiones

Unicidad del límite

Límite de la sucesión comprendida

Operaciones con límites

Límite de la suma

Definición

Sucesiones equivalentes

Definición

Sucesión acotada

Teorema

Teorema

Definición

Par de sucesiones monótonas convergentes

Propiedad

Todo PSMC tiene frontera

El número e

Etiquetas

Novedades